DILATACIÓN TÉRMICA
DILATACIÓN LINEAL
Es aquella en la cual predomina la variación en una única dimensión, o sea, en el ancho, largo o altura del cuerpo. El coeficiente de dilatación lineal, designado por αL, para una dimensión lineal cualquiera, se puede medir experimentalmente comparando el valor de dicha magnitud antes y después:
Donde  , es el incremento de su integridad física cuando se aplica un pequeño cambio global y uniforme de temperatura
, es el incremento de su integridad física cuando se aplica un pequeño cambio global y uniforme de temperatura 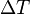 a todo el cuerpo. El cambio total de longitud de la dimensión lineal que se considere, puede despejarse de la ecuación anterior:
a todo el cuerpo. El cambio total de longitud de la dimensión lineal que se considere, puede despejarse de la ecuación anterior:
 , es el incremento de su integridad física cuando se aplica un pequeño cambio global y uniforme de temperatura
, es el incremento de su integridad física cuando se aplica un pequeño cambio global y uniforme de temperatura 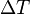 a todo el cuerpo. El cambio total de longitud de la dimensión lineal que se considere, puede despejarse de la ecuación anterior:
a todo el cuerpo. El cambio total de longitud de la dimensión lineal que se considere, puede despejarse de la ecuación anterior:
Donde:
- α=coeficiente de dilatación lineal [°C-1]
- L0 = Longitud inicial
- Lf = Longitud final
- T0 = Temperatura inicial.
- Tf = Temperatura final
- Ejercicio resuelto
- Los rieles de una vía de tren de acero, tienen 1500m de longitud. ¿Qué longitud tendrá cuando la temperatura aumente de 24ºc a 45ºc?
- Datos:
–> Longitud Inicial
–> Longitud Final
–> Temperatura Inicial
–> Temperatura Final
–> Coeficiente de dilatación lineal del Acero.
Hemos elegido acero, porque el problema nos pide que son vías del ferrocarril de acero.Lo único que haremos será sustituir nuestros datos, en la fórmula final.Pero antes de sustituir, debemos saber cual es el valor de la diferencial de temperatura, para poder meterla en la fórmula, esa diferencial es la resta de la temperatura más alta, con la temperatura más baja.Ahora si, a sustituir en la fórmula.Si observamos, las vías del tren se han dilatado solo .3465 metros, es decir 346.5 milímetros, muy poco, pero significativo para la distancia entre las juntas de riel.
DILATACIÓN SUPERFICIAL
Es aquella en que predomina la variación en dos dimensiones, o sea, la variación del área del cuerpo debido a la intervención de un cambio de temperatura.
El coeficiente de dilatación superficial es cuando los sólidos con un área de un metro cuadrado se les aumenta 1ºc su temperatura, varia en su área de manera constante
La formula con la que se mide la dilatación superficial es:
Sf-Si Sf = Si [1 + g (Tf- Ti)]
Donde:
El coeficiente de dilatación superficial es cuando los sólidos con un área de un metro cuadrado se les aumenta 1ºc su temperatura, varia en su área de manera constante
La formula con la que se mide la dilatación superficial es:
Sf-Si Sf = Si [1 + g (Tf- Ti)]
Donde:
g = coeficiente de dilatación superficial (1/ºc).
Sf = Superficie final (m2)
Si = Superficie inicial (m2)
Tf = Temperatura final (ºC)
Ti = Temperatura inicial (ºC)
Ejercicio resuelto
Una placa de vidrio de 10x10 cm incrementa su temperatura de 17ºc a 50ºc ¿Cual es su incremento superficial?
Datos:
Ti = 17ºc
Tf = 50ºc
Si = 10x10cm= 1m2
g = 1.8x10-5 1/ºc
Sustitución de datos:
ΔS= 1m2
[1.8x10-5 1/ºc (50ºc – 17ºc)]
ΔS= 1m2
[1.8x10-5 1/ºc (33ºc)]
ΔS= 0.00594m2
DILATACIÓN VOLUMETRICA
Es aquella en la que predomina la variación en tres dimensiones, o sea, la variación del volumen del cuerpo, este fenómeno se ve dado en el estado liquido "La dilatación volumetrica que se presenta en un liquido es directamente proporcional a la diferencia de volumenes en inversamente proporcional al volumen inicial multiplicado por la diferencia de temperaturas".
El coeficiente volumetrico es cuando las sustancias con un volumen inicial de un metro cubico se les aumenta 1ºc su temperatura, varían su volumen de manera constante.
Formula que se utiliza para la dilatación volumetrica es:
β = Vf-Vi
Vi (Tf-Ti) β = Vi [1 + β (Tf-Ti)]
Donde:
β = Coeficiente superficial (1/ºc)
Vf = Volumen final (m3)
Vi = Voluemen inicial (m3)
Tf = Temperatura final (ºC)
Ti = Temperatura inicial (ºC)
Ejercicio resuelto
Antonio un litro de alcohol etílico (vino blanco) en la estufa para calentarla, ya que prepararía la cena de navidad; el alcohol estaba a 15ºc. Después de unos minutos, midió la temperatura y el termómetro marcó 85ºc. Determina cuanto varía el volumen de alcohol.
Datos:
Sustitución de la formula:
*Vf = 0.001m3 [1 + 746x10-6 1/ºc (85ºc - 15ºc)]
Vf = 0.001m3 [1 + 746x10-6 1/ºc (70)]
Vf = 0.00105222 m3
Δv = 5.22x10-5 m3
Antonio un litro de alcohol etílico (vino blanco) en la estufa para calentarla, ya que prepararía la cena de navidad; el alcohol estaba a 15ºc. Después de unos minutos, midió la temperatura y el termómetro marcó 85ºc. Determina cuanto varía el volumen de alcohol.
Datos:
β alcohol =746x10-6 1/ºc
Vf = ?
Vi = 0.001m3
Tf = 85 ºc
Ti = 15ºc
Δv = ?Sustitución de la formula:
*Vf = 0.001m3 [1 + 746x10-6 1/ºc (85ºc - 15ºc)]
Vf = 0.001m3 [1 + 746x10-6 1/ºc (70)]
Vf = 0.00105222 m3
Δv = 5.22x10-5 m3
DILATACIÓN IRREGULAR DEL AGUA
La dilatación irregular del agua se produce entre los 0ºC y 4ºC, ya que en este intervalo termico se comporta al revés, es decir, el agua se dilata al enfriarse, y se contrae al calentarla. Por eso el agua ocupa menos volumen es el agua a 4ºC.
Este comportamiento se puede notar cuando se congela un charco de agua, el proceso de congelamiento de esté es lento y comienza de arriba hacia abajo, cuando la temperatura de la atmosfera bajo de 8ºC a 6ºC, el agua que se encuentra.


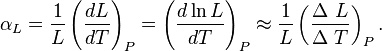
![L_f = L_0 [1 +\alpha_L (T_f - T_0)]\;](https://upload.wikimedia.org/math/4/d/8/4d8d9e521d59aa36de0d776706db3b16.png)



No hay comentarios.:
Publicar un comentario